I decided to revisit the Batman Equation briefly, but this time at a Python approach, instead of Matlab. The languages are close enough that it shouldn't take very to plug the info in and run...or so I thought.
Giving it an Initial Go
It started out easy enough. From my Batman Equation Gist I grabbed the 6 equations and pasted them into batman.py to run and hope it worked. First thing I had to do was change the syntax for the power function. So a simple Find/Replace of "^" to "**" cleaned that up quickly. I also removed all the semicolons from the end-on-lines.
Next I had to make sure I had everything I needed:
import matplotlib.pyplot as plt #To be capable of plotting from scipy import sqrt
I also had to think about how to handle the equations properly. Since Python doesn't have a qualifier like Matlab's sym x y, we'll give Python a complete grid of x and y points to work with.
from numpy import meshgrid from numpy import arange xs = arange(-7.25, 7.25, 0.01) ys = arange(-5, 5, 0.01) x, y = meshgrid(xs, ys)
This should be essentially it. Now we plot:
for f in [eq1,eq2,eq3,eq4,eq5,eq6]: plt.contour(x, y, f, [0]) plt.show()
WHAT!?
Problems
Complex Numbers
So the first problem I had was the simple one. I was using sqrt from scipy which handles complex numbers and returns the real portion. I needed to remain in the real subset of numbers, so I change this line to:
from numpy import sqrt
Success?
No...
The Hard Part
So it looks close, but the "wings" are missing half the line and it's at 0. So first think I thought of is that the complex-to-real is blowing things up. So I took 'eq1' and tore it apart. Basically it's an ellipse with the center section cut out. So I carved it up into the elements to find the offending piece.
eq1 = (x/7)**2+(x/3)**2-1 # Plots ellipse beautifully eq1 = ((x/7)**2*sqrt(abs(abs(x)-3)/(abs(x)-3))+(x/3)**2-1 # Cuts the middle out and looks good eq1 = ((x/7)**2*sqrt(abs(abs(x)-3)/(abs(x)-3))+(y/3)**2*sqrt(abs(y+3/7*sqrt(33))/(y+3/7*sqrt(33)))-1) # Fails
So the offending block sqrt(abs(y+3/7*sqrt(33))/(y+3/7*sqrt(33))) is what's causing problems.
Just using the IPython interpreter I laboriously realized that Python was evaluating 3/7 as 0. Which of course we all know is not true. So after a wealth of internet searching and more, I found that I needed to force Python out of floor division for integers. Totally something new to me and can't believe it took me so long to find out. Turns out Python 3 corrects this, but I'm using 2.7.
I first thought I had was to add .0 to all my integers in my equations, but found that adding this took care of it for me:
from __future__ import division
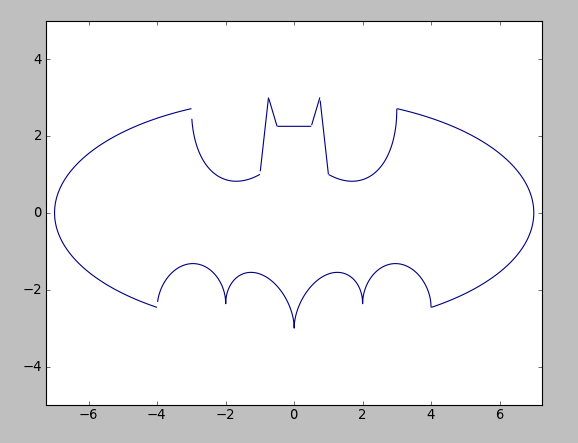
Success!

